CoppeliaSim Youbot Pick and Place simulation
Simluation of youBot mobile manipulator in Coppeliasim picking up a cube from one location and placing it down at a final position in Python.
Overview
This software plans a trajectory of the end effector of the youBot mobile manipulator (a mobile base with four mecanum wheels and a 5R robot arm), to pick up a block from a specified location, carry it to a final location and place it down. It also performs odometry as the chassis moves and feedback control to drive the youBot to pick up the block. The final output of the software will be a comma-separated values (csv) text file that specifies the configurations of the chassis and the arm, the angles of the four wheels, and the state of the gripper (open or closed) as a function of time. The initial configuration (the chassis phi, chassis x, chassis y, J1, J2, J3, J4, J5, W1, W2, W3, W4, gripper state = 0, 0.2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0), used is (x, y, 𝜃) = (0.2, 0, 0). The initial block configuration is at (x, y, 𝜃) = (1m, 0m, 0 rad) and the final block configuration is at (x, y, 𝜃) = (0 m,-1m, -π/2 rad). In ‘New Task’, the initial block configuration is at at (x, y, 𝜃) = (0.5m, 1.0m, 0 rad) and the final block configuration is at (x, y, 𝜃) = (0.5m, -1.5m, -π/2rad). The results were obtained using a feedforward PI controller tuned individually for each task.
Algorithm description
The NextState function employs the first-order Euler method to determine the robot’s configuration at the next time step.
The TrajectoryGenerator function is responsible for generating the reference trajectory for the end-effector frame {e}. This trajectory consists of eight concatenated trajectory segments, as described below. Each trajectory segment begins and ends at rest.
Across 8 stages in the simulation, the process unfolds as follows:
- A trajectory to move the gripper from its initial configuration to a “standoff” configuration a few cm above the block.
- A trajectory to move the gripper down to the grasp position.
- Closing of the gripper.
- A trajectory to move the gripper back up to the “standoff” configuration.
- A trajectory to move the gripper to a “standoff” configuration above the final configuration.
- A trajectory to move the gripper to the final configuration of the object.
- Opening of the gripper.
- A trajectory to move the gripper back to the “standoff” configuration.
Throughout each stage, the algorithm uses the ScrewTrajectory function from the modern robotics python library. This function, utilizing the third-order or fifth-order polynomial time-scaling method, takes the start and end transformations of the gripper as inputs. It generates a discrete trajectory in the form of a list of end-effector transformation matrices. The FeedbackControl function is instrumental in computing the kinematic task-space feedforward plus feedback control law.
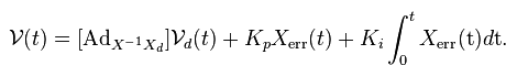
Results
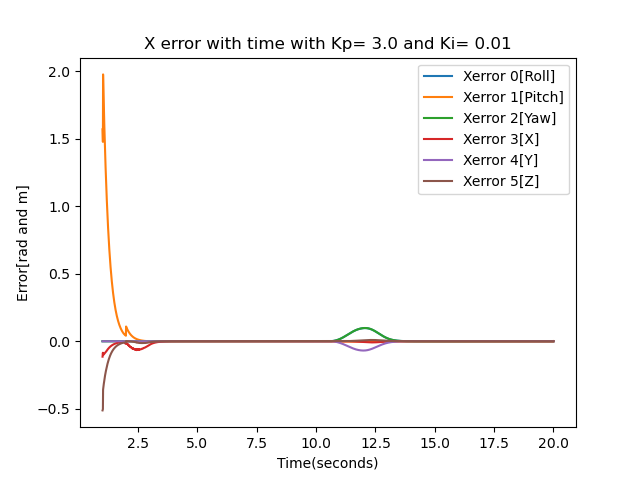
Best
The best results were obtained by tuning the proportional gain(Kp) to 3.0 and the integral gain(Ki) to 0.01. As seen from the error plot there is a tiny error in the middle but converges after that. The initial block configuration is at (x, y, 𝜃) = (1m, 0m, 0 rad) and the final block configuration is at (x, y, 𝜃) = (0 m,-1m, -π/2 rad).
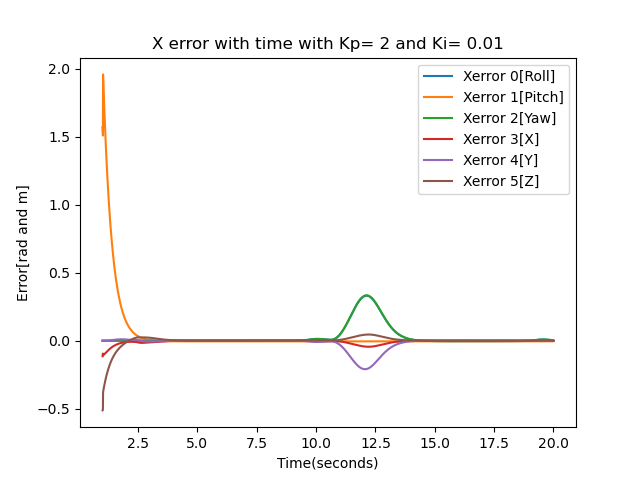
Overshoot
The overshoot results were obtained by tuning the proportional gain(Kp) to 2.0 and the integral gain(Ki) to 0.01. As seen from the error plot there is a tiny error in the middle but converges after that. It overshoots slightly in the beginning as seen from the red loop but converges after that. The initial block configuration is at (x, y, 𝜃) = (1m, 0m, 0 rad) and the final block configuration is at (x, y, 𝜃) = (0 m,-1m, -π/2 rad).
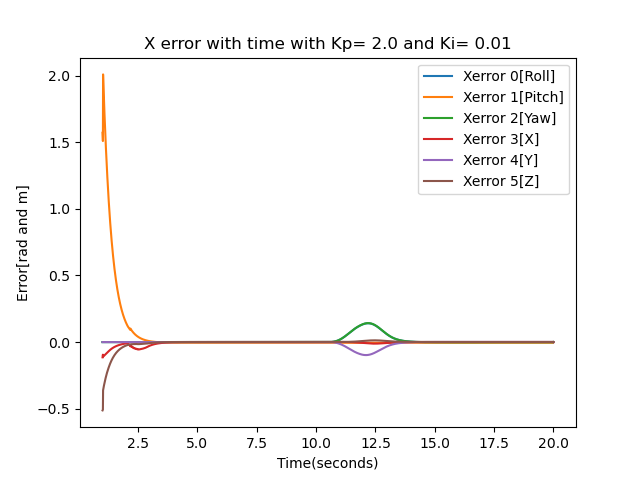
newTask
The newTask results were obtained by tuning the proportional gain(Kp) to 2.0 and the integral gain(Ki) to 0.01. As seen from the error plot there is a tiny error in the middle but converges after that. The initial block configuration is now at (x, y, 𝜃) = (0.5m, 1.0m, 0 rad) and the final block configuration is at (x, y, 𝜃) = (0.5 m,-1.5m, -π/2 rad).