Explainable AI for Hand Gesture Recognition
Explainable AI to classify hand gestures from sEMG signals using shapley values and transfer learning.
Table of Contents
Overview
Model Architecture with Shapley Feedback
Transfer Learning
Conclusion and Future Work
Overview
This project aims to improve upon a previously developed hand gesture recognition system by incorporating Explainable AI techniques. The goal is to enhance the model’s interpretability and transparency.
Model Architecture with Shapley Feedback
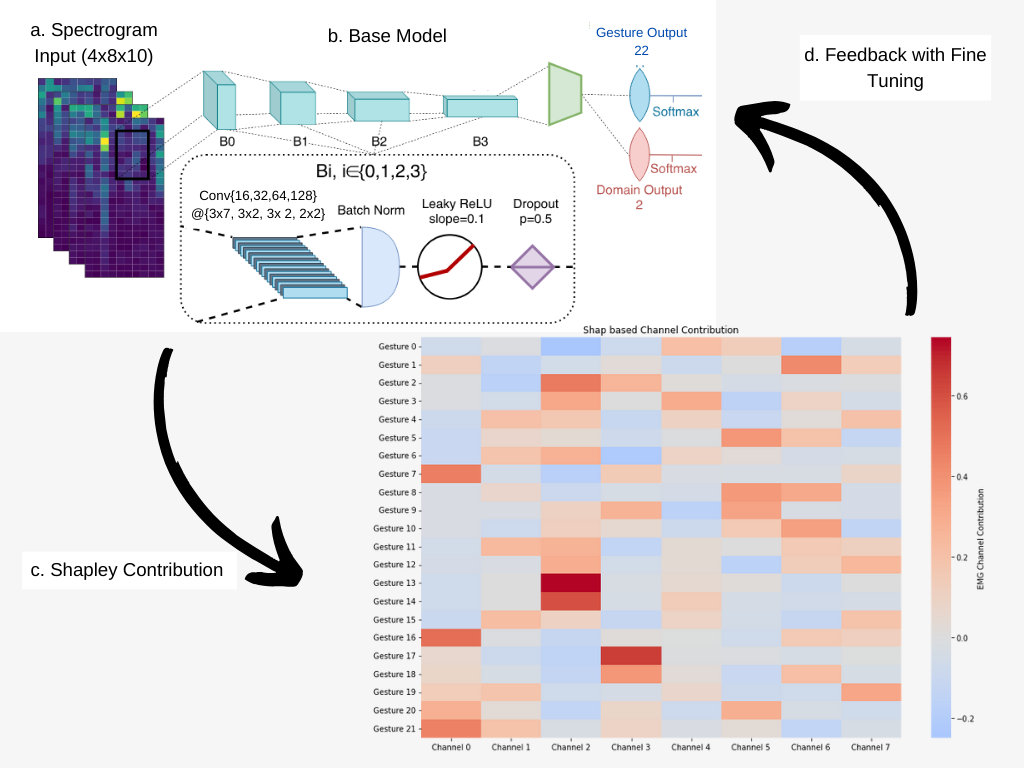
Model architecture for Shapley Feedback Based Convolutional Neural Network
a. Spectrogram Input(Dataset)
The dataset was a publically available dataset of hand gestures, based on this paper and code. The dataset comprises surface EMG signals recorded from 5 participants over 10 days, using the Myo Armband (Thalmic Labs), a wearable sensor with 8 dry electrodes designed for ease of use without skin preparation. Signals were captured at three sensor positions—neutral, 8-mm inward rotation, and 8-mm outward rotation—randomly across 30 days. Each participant performed 22 gestures, including single- and two-degree-of-freedom wrist and hand motions, with 4 repetitions per gesture daily. EMG signals, sampled at 200 Hz and high-pass filtered at 15 Hz, were segmented using a sliding window of 250 ms with 80% overlap, capturing 1.5-second trials representing muscle activity during gestures. The dataset structure, shaped as 4 × 22 × 26 × 8 (repetitions × gestures × segments × channels). This is then processed into formatted spectrograms of shape (4x8x10) which represents (time x channels x frequency) for the model input.
b. Base Model (ConvNet)
The original model based on this paper is a small, simple ConvNet architecture that takes spectrogram inputs and performs gesture classification. The ConvNet’s architecture contains four blocks followed by a global average pooling and two heads. The first head is used to predict the gesture held by the participant. The second head is only activated when employing domain adversarial algorithms. Each block encapsulates a convolutional layer, followed by batch normalization, leaky ReLU and dropout.
c. Shapley Contribution
Shapley Values
Shapley values are a method from cooperative game theory that assigns a value to each feature based on its contribution to the model’s prediction.
Think of each sensor channel as a player on a team. Shapley values help us figure out how much each ‘player’ (channel) contributes to the team’s success (the model’s correct classification). This means we can identify which muscle signals are most important for recognizing a given gesture.
The paper I used to incorporate the Shapley value method introduces a method leveraging Shapley values for understanding and enhancing gesture recognition from sEMG signals. By treating each electrode channel as a “player” in a cooperative game, the Shapley value (\( \phi_n \)) quantifies each channel’s contribution to recognizing gestures.
Total Contribution
The total contribution of all channels ((C)) is calculated as the difference in model output with and without all input channels:
\(C = f(\text{all channels}) - f(\emptyset)\)
- \( C \) : Total contribution of all electrode channels in gesture recognition.
- \( f(\text{all channels}) \) : Model output when all channels’ signals are used as input.
- \( f(\emptyset) \) : Model output when no channel signal is used as input (zero input).
Shapley Value
The Shapley value for a channel (n) is computed by averaging its marginal contribution across all possible coalitions (\( (S \subseteq N) \)):
\(\phi_n = \sum_{S \subseteq (N \setminus \{n\})} \frac{|S|! \cdot (|N| - |S| - 1)!}{|N|!} \cdot \left[f(S \cup \{n\}) - f(S)\right]\)
- \( \phi_n \) : Shapley value of the \( n \)-th channel, indicating its contribution to gesture recognition.
- \( N \) : Total set of electrode channels.
- \( S \) : Subset of channels excluding channel \( n \).
- \( \vert S \vert \) : Number of channels in subset \( S \).
- \( f(S \cup \{n\}) \) : Model output when subset \( S \) plus channel \( n \) is used as input.
- \( f(S) \) : Model output when only subset \( S \) is used as input.
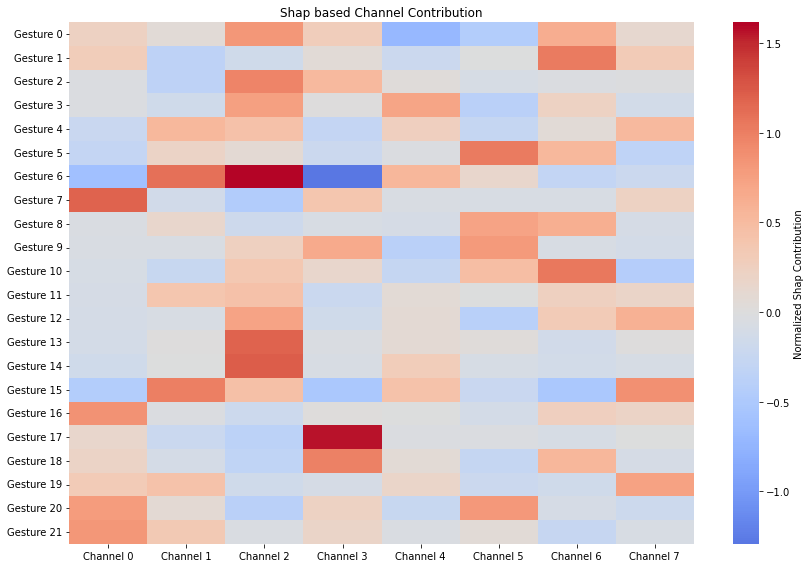
Shapley values for each EMG channel, indicating their relative importance for gesture recognition
The above image shows the Shapley values for each EMG channel, indicating their relative importance for gesture recognition. For example Channel 2 is positively contibuting to the model in recognizing gesture 6 while Channel 3 is negatively contributing to recognizing gesture 6.
d. Feedback with Fine Tuning(Network Adaptation)
The feedback mechanism applies the Shapley contribution ratios to dynamically adjust the weights of the first convolutional layer in the neural network, emphasizing the importance of specific EMG channels for recognizing gestures. For each gesture \( g \), the Shapley contribution ratio for each channel \( c \) is given as \( S_{g,c} \), indicating the relative importance of that channel for the gesture. This value is used to compute a scaling factor for adjusting the convolutional kernel weights:
\[ \text{scaling_factor} = 1.0 + S_{g,c} \]
Channels with higher \( S_{g,c} \) are amplified, while those with lower or negative \( S_{g,c} \) are de-emphasized. Specifically, the kernel weights \( W_{k,h,w} \) for the \( k \)-th filter, at height \( h \), and width \( w \), are scaled for each channel as:
\[ W_{k,h,w,c} \leftarrow W_{k,h,w,c} \times \text{scaling_factor} \]
where \( c \) corresponds to the EMG channel index.
After modifying the kernel weights, the model is fine-tuned to adapt the network to the new weighted input representations. All layers except the final fully connected layer (\( \mathbf{W}{\text{output}} \)) are frozen to preserve the learned feature hierarchies. The fine-tuning loss is minimized using the categorical cross-entropy loss:
\[\mathcal{L} = -\frac{1}{N} \sum_{i=1}^{N} \sum_{j=1}^{C} y_{i,j} \log \hat{y}_{i,j}\]where \( y_{i,j} \) and \( \hat{y}_{i,j} \) are the true and predicted probabilities for class \( j \), and \( N \) is the batch size.
The model is trained using early stopping, and the version with the lowest validation loss \( \mathcal{L}_{\text{val}} \) is saved. By dynamically adjusting the input weights based on Shapley contributions and fine-tuning the model, the feedback mechanism ensures that the network emphasizes the most important channels for gesture recognition while preserving its generalization ability.
Transfer Learning Problem
Imagine learning to recognize certain gestures from one group of people (source) and then trying to recognize them in a different group (target). Transfer Learning is like ‘teaching’ the model to use what it learned previously while adjusting to the differences in the new group, even if the model hasn’t seen that exact scenario before.
The original model based on this paper was trained using this method. This is particularly effective when the target domain lacks sufficient labeled data, as it allows the model to leverage knowledge learned from the source domain to generalize better in new contexts.
The source domain consists of labeled surface EMG signals collected from specific users on particular days at a fixed sensor position (e.g. neutral position). The target domain involves unlabeled EMG signals from different users recorded on multiple days but at the same sensor position. The variability between users and recording days introduces challenges due to physiological differences and temporal variations in the EMG signals.
In myoelectric control systems, labeled data from user calibration sessions is essential but transient, as sEMG signals degrade over time, requiring frequent recalibration to maintain performance. However, during regular use, unlabeled data is continuously generated, making unsupervised domain adaptation a natural solution, with the calibration session as the labeled source and ongoing usage data as the unlabeled target.
The study, demonstrates how transfer learning can improve gesture classification accuracy across users and days without requiring additional labeled data. While SpectroConvNet combined with DANN(Domain Adversarial Neural Network), fed into SCADANN achieves impressive performance in adapting to new users and days, it functions as a black-box model, meaning its internal workings and decision-making processes are not easily interpretable. This lack of transparency makes it challenging to understand which features or patterns in the EMG signals are driving the predictions.
Shapley Feedback for Transfer Learning
The previous approach does not take into account transfer learning, hence a novel approach has to be developed to incorporate Shapley feedback into the transfer learning process. The goal is to enhance the model’s interpretability and transparency while maintaining its performance in adapting to new users and days.
This is done as follows:
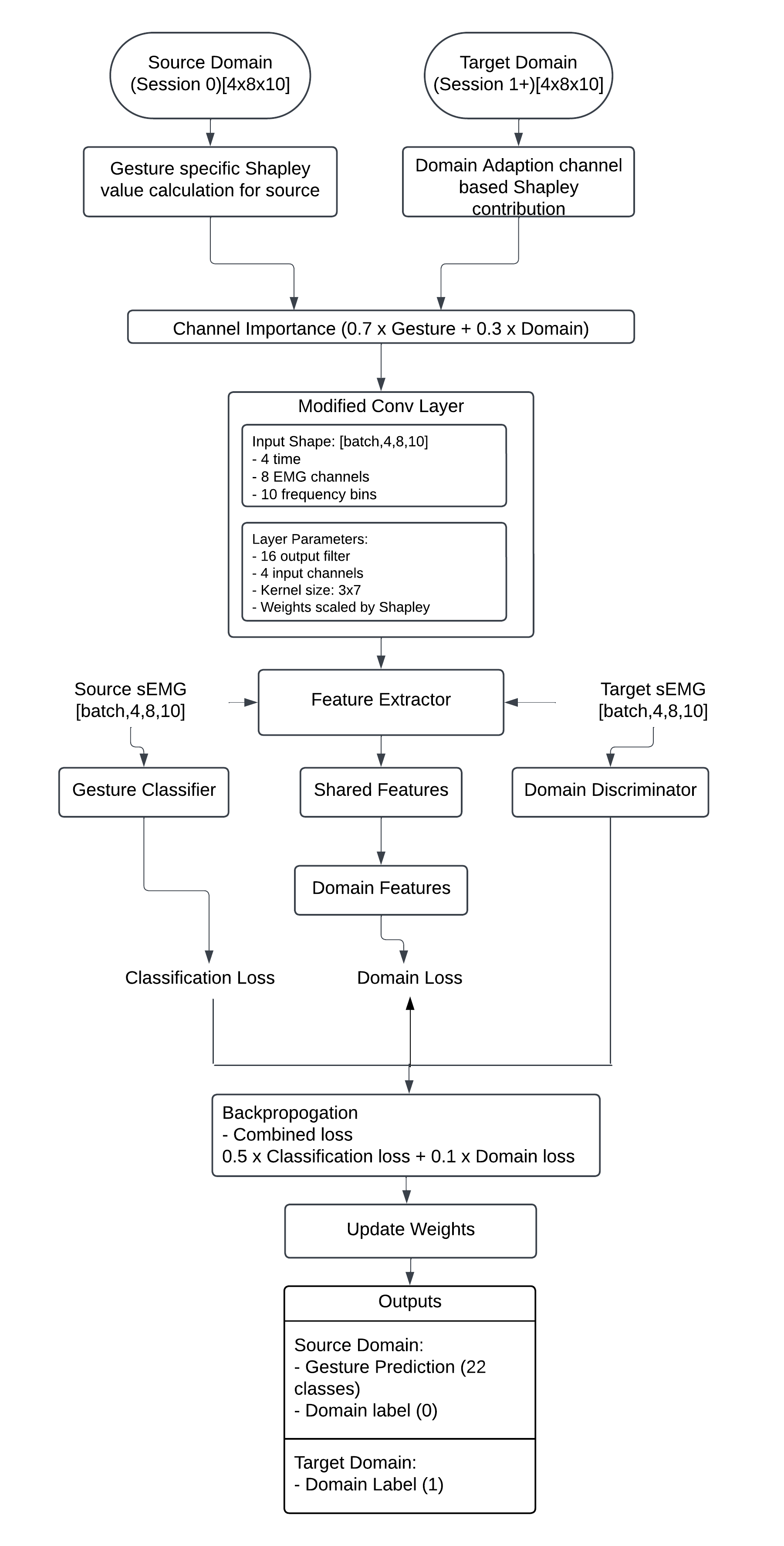
Training architecture for Shapley Feedback Based Domain Adversarial Transfer learning
The training process incorporates Shapley values to improve the performance of the Domain-Adversarial Neural Network (DANN) by dynamically modifying the model’s weights based on channel contributions for both gesture recognition (source domain) and domain adaptation (target domain).
The main difference in the previous approach and the transfer learning approach is the calaculation of shapley values. In this case, shapley values are calculated for both source and target domain as follows:
Source Domain: Gesture-Specific Contributions
For gesture classification, Shapley values were computed for each gesture \( g \) using the source domain data:
Marginal Contribution for a Subset: For a channel \( n \) (or a group of channels defined by a kernel window), the marginal contribution is:
\[\Delta f(S, n) = f(S \cup \{n\}) - f(S)\]Where:
- \( f(S \cup \{n\}) \): Gesture classification accuracy when both \( S \) and \( n \) are active
- \( f(S) \): Gesture classification accuracy when only \( S \) is active
Shapley Value Estimation: Since enumerating all subsets \( S \) is computationally expensive, the Shapley value is approximated by sampling:
\[\phi_{n,g} \approx \frac{1}{M} \sum_{i=1}^M \Delta f(S_i, n)\]Where \( S_i \) is a randomly sampled subset, and \( M \) is the number of samples.
Target Domain: Domain Adaptation Contributions
For domain adaptation, Shapley values were computed using the target domain data:
Domain Classification Accuracy: Let \( f_d(S) \) represent the domain classification accuracy when only the channels in \( S \) are active:
\[\Delta f_d(S,n) = f_d(S \cup \{n\}) - f_d(S)\]Shapley Value for Domain Adaptation:
\[\phi_{n,d} \approx \frac{1}{M} \sum_{i=1}^M \Delta f_d(S_i, n)\]Combining Gesture and domain contributions, the first convolutional layer’s weights were adjusted based on the calculated Shapley values
The combined Shapley value for each channel \( n \) is:
\[\phi_n = \alpha \cdot \phi_{n,g} + (1 - \alpha) \cdot \phi_{n,d}\]Where:
- \( \phi_{n,g} \): gesture-specific contribution
- \( \phi_{n,d} \): domain-specific contribution
- \( \alpha \): hyperparameter balancing gesture and domain contributions
These scaling factors were applied to the kernel weights \( W_{k,h,w} \) for the respective channels.
This approach increased the accuracy of the previous DANN model by 2% and also provided a more interpretable model.
Results before Shapley Feedback
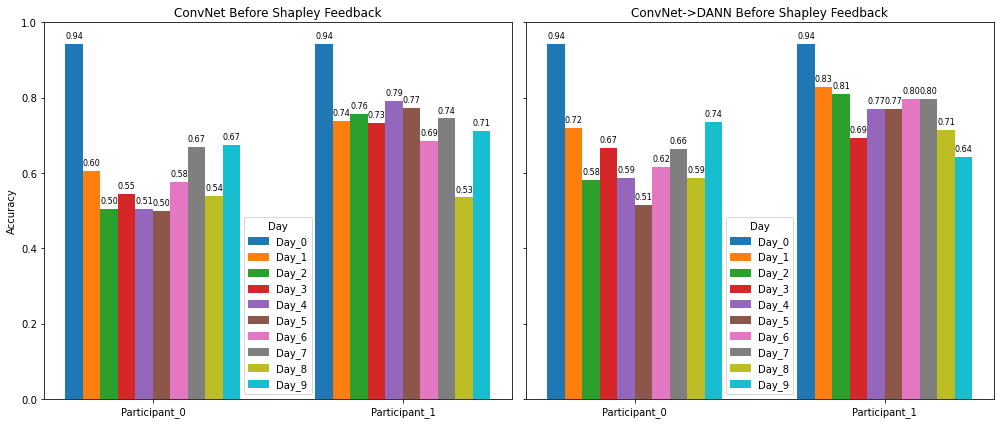
Participant Model Performance by Day Prior to Shapley Feedback
Results after Shapley Feedback
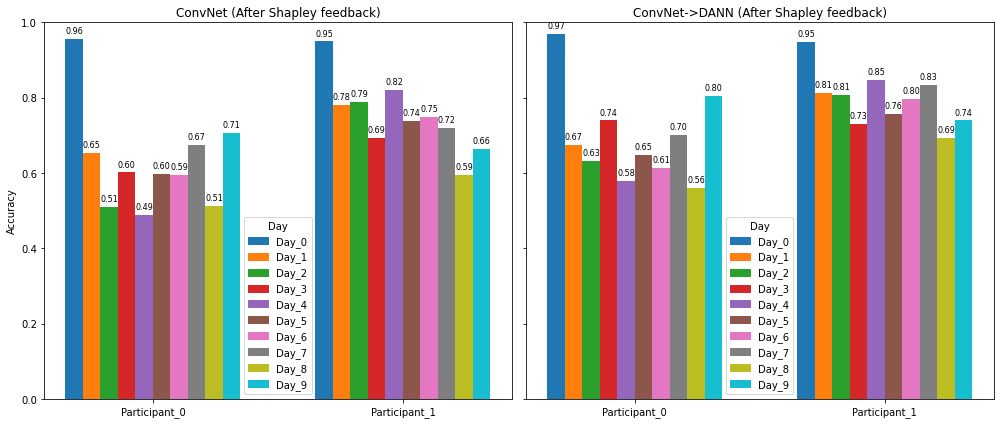
Participant Model Performance by Day After Shapley Feedback
Overall Comparison
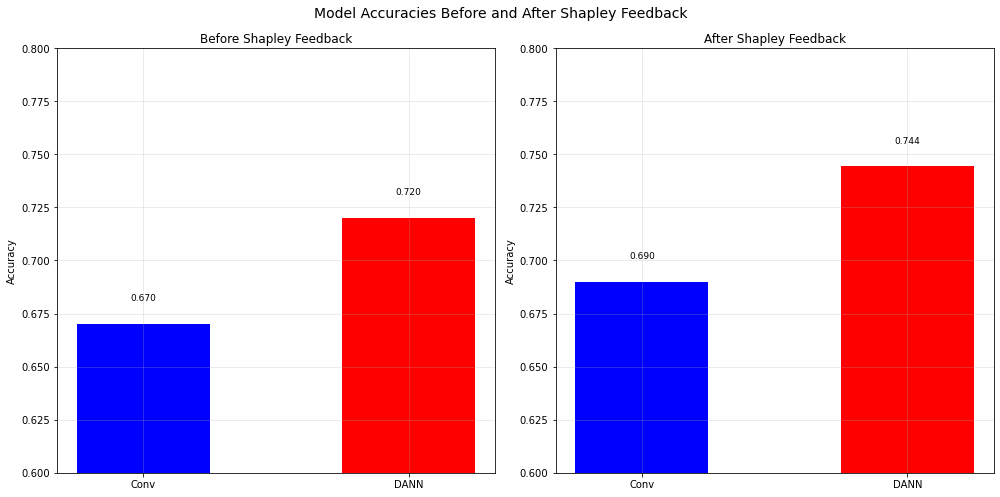
Overall Accuarcy comaprison
The above graphs demonstrate clear improvements in model accuracy following the incorporation of Shapley feedback. After implementation, both architectures showed consistent performance gains of approximately 2%, with ConvNet improving from 67% to 69% (before transfer learning), and DANN advancing from 72% to 74% (transfer learning). This parallel improvement suggests the effectiveness of Shapley feedback across different model architectures. Throughout the experiments, Participant_1 exhibited notably better and more stable performance compared to Participant_0 across both models and time periods. The introduction of Shapley feedback not only enhanced overall accuracy, but also contributed to more stable day-to-day performance variations, with this stabilizing effect being particularly pronounced in the DANN model’s results.
Conclusion and Future Work
Key Takeaways:
- Improved Interpretability: Using Shapley values makes it clearer which EMG channels (muscle signals) matter most for recognizing gestures.
- Better Accuracy: Applying Shapley-based feedback improved the ConvNet model from 67% to 69% accuracy and the DANN model from 72% to 74%.
- Stable Performance Over Time: The day-to-day variability in accuracy decreased, making the model more reliable.
- Works Across Models: Both the simpler ConvNet and the more complex DANN architecture benefited from Shapley feedback, showing this approach is versatile.
Incorporating Shapley values into the gesture recognition pipeline not only improved model performance in domain adaptation scenarios but also enhanced the interpretability of the underlying decision making process. By identifying critical EMG channels for both gesture recognition and domain adaptation, this approach provides deeper insights into the model’s behavior.
Future work could involve exploring more efficient Shapley value approximation methods to reduce computational overhead, integrating additional explainability tools to complement Shapley analyses, and extending the framework to more complex, multi-sensor datasets. Additionally, investigating real-time adaptability, where Shapley values dynamically adjust weights as new data arrives, could help create continuously learning systems capable of maintaining high performance even as user conditions, environments, or sensor placements change over time.
References
Acknowledgements
Thank you to Dr. Matthew Elwin and Professor Hongchul Sohn for their guidance and support throughout this project.